Game’s Anatomy 4: To the render mobile!

Witam w części czwartej naszego przewodnika po anatomii gier. W części drugiej rozmawialiśmy o algebrze liniowej, a w trzeciej rozpoczęliśmy podróż od trójwymiarowej sceny do kolorowych pikseli na ekranie. Zatrzymaliśmy się w momencie, kiedy już było wiadomo co będziemy renderować i mieliśmy właśnie przenieść się z robotą z CPU na kartę graficzną. Dzisiaj zrobimy ten krok w nieznane.

Najpierw będziemy rozkładać model na części pierwsze i poprzestawiamy w nim wszystko tak, żeby wyglądał jak powinien. Potem będziemy brać z niego po jednym trójkącie, a następnie rasteryzować, interpolować i kolorować, a wszystko po to, żeby na naszym monitorze wyświetliła się jedna, mała, kolorowa kropeczka. A potem następna i następna. A to wszystko niemal jednocześnie. No to zapraszam.

Poprzednie części cyklu. Pierwsza traktowała o zupełnie innym temacie, ale drugą i trzecią polecam przeczytać przed przystąpieniem do niniejszego tekstu:

• Game’s Anatomy 1 — fizyka w grach
• Game’s Anatomy 2 — podstawowe pojęcia z grafiki 3D
• Game’s Anatomy 3 — początek renderingu

Rozszczepienie modelu, czyli wierzchołek góry shaderowej

Kiedy już model znajdzie się w karcie graficznej, zaczyna się robota dla shaderów. Czym jest shader? Po prostu krótkim (przynajmniej w porównaniu do reszty gry) programem komputerowym, pisanym tak samo jak pozostałe elementy gry i to nawet w bardzo podobnym języku. Od reszty silnika itd. różni się przede wszystkim tym, że odpalany jest, oczywiście, na karcie graficznej. Ten fakt wymaga natomiast od shaderów by działały na trochę innych zasadach niż zwykłe programy i spełniały nieco inny szereg warunków. Ale o tym później.

Więc co dzieje się z meshem rzuconym na pożarcie karcie graficznej? Najpierw model rozbijany jest na verteksy, które z kolei są pojedynczo przekazywane do vertex shadera. Vertex shader otrzymuje pozycję (czyli współrzędne) werteksu w przestrzeni lokalnej obiektu oraz macierz przekształcenia z tejże do właściwej przestrzeni kamery. Dla jasności i przypomnienia dodam, że na werteksy się nie patrzy, tylko się je przestawia. To obiekty matematyczne w konkretnych punktach danej przestrzeni. W przestrzeni lokalnej obiektu werteksy mają takie współrzędne, że budują obiekt w jego zamierzonej przez grafika formie. Aby widzieć go z punktu widzenia kamery musimy przekształcić werteksy do przestrzeni kamery, a więc poprzestawiać je w inne punkty tak, by zbudowały obiekt o właściwym kształcie — wyglądający jak widziany z danego miejsca przez kamerę o określonych właściwościach. Do tego właśnie potrzebna jest macierz, czyli wynalazek zjadający współrzędne w jednej przestrzeni, przeżuwający je i wypluwający współrzędne w innej przestrzeni.

Przekształcenie do kamery może zawierać perspektywę lub nie, zależnie od wybranego rodzaju kamery. Na tym jednak historia się nie kończy. Programista shaderów ma również do dyspozycji wiele innych macierzy przekształceń, np. z przestrzeni obiektu do przestrzeni globalnej, z globalnej do jakiegoś światła itd. Najczęściej są one dostarczone przez silnik i nie ma potrzeby ich ręcznie obliczać.

Ważne jest, że w materii tego jak shader wyznaczy te współrzędne dla przestrzeni kamery panuje całkowita dowolność. Jeśli ktoś chce, to może tam wstawić całkowicie losowe wartości — oczywiście nie ma to najmniejszego sensu, bo w rezultacie otrzymamy papkę przypominającą niektórej przejawy „sztuki” nowoczesnej. Z tego względu programiści często ograniczają się do przekształcenia obiekt-do-kamery, jednak nic nie stoi na przeszkodzie, żeby np. dodawać do uzyskanych w ten sposób wektorów losowe wartości, uzyskując tym samym np. efekt falowania powierzchni. Można również, zamiast wartości losowych, dodawać wartości zapisane na jakiejś teksturze.

Wracając na chwilę do matmy, to wszystko jest możliwe właśnie dlatego, że nie mówimy o fizycznych obiektach, które się ogląda z różnych punktów, tylko o chmurze wierzchołków, którch oglądanie z określonego miejsca oznacza ni mniej ni więcej jak poprzestawianie ich w odpowiednie miejsca względem początku układu współrzędnych (leżącego, np. w środku kamery).

Efektem pracy vertex shadera są zawsze współrzędne dokładnie jednego wetreksu w przestrzeni kamery, choć mogą do tego dojść też inne wartości dla tego werteksu — np. koordynaty tekstur czy kolor, które później są interpolowane i podawane do fragment shadera po rasteryzacji. O tym za chwilę, więc nie martwcie się, jeśli nie rozumiecie co drugiego słowa.

Rasteryzacja i kolejny fragment historii o shaderach

Kiedy już powiemy karcie graficznej gdzie ma sobie wsadzić… um, znaczy ustawić wszystkie werteksy tak, żeby obiekt wyglądał jak widziany przez kamerę (taką czy inną), rozpoczyna się proces rasteryzacji i kolorowania fragmentów, w którym ogromną rolę do odegrania mają z kolei fragment shadery — zwane częściej pixel shaderami, co jest nazwą o tyle bardziej znajomą co mniej precyzyjną.

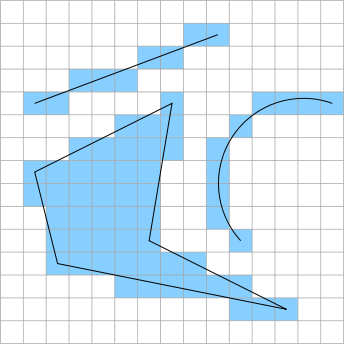
Rasteryzację definiuje się jako odwzorowywanie prymitywu na ekranie o skończonej rozdzielczości. Obrazowo mówiąc, jest to proces podobny do narysowania trójkąta na kartce w kratkę, a następnie zamalowania wyłącznie tych kratek, które w całości lub w wystarczającej części znajdują się w obrębie tego trójkąta.

I Ty możesz rasteryzować!

Karta graficzna wyszukuje więc takie właśnie piksele, które od tego momentu nazywamy „fragmentami”, gdyż stanowią fragmenty odwzorowania prymitywu, i pojedynczo przekazuje je do fragment shadera. Shader natomiast koloruje je zgodnie z wolą programistów i grafików. Przekazanie następuje wraz z interpolowanymi parametrami werteksów wchodzących w skład trójkąta, w którym leży dany fragment. Te parametry to przede wszystkim, jak już kilkukrotnie mówiłem, koordynaty tekstur i kolor.

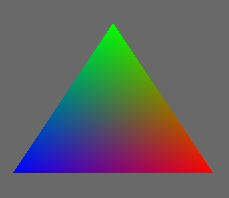
Podejrzewam, że nie wszyscy wiecie co to takiego interpolacja i czym się ją je. Spieszę wyjaśnić, że nie ma to nic wspólnego z Interpolem. Chodzi tutaj o (uwaga) wyznaczanie wartości pośredniej w konkretnym punkcie pomiędzy znanymi wartościami skarajnymi położonymi, w tym wypadku, na wierzchołkach trójkąta. Interpolację koloru na trójkącie przedstawia poniższy obrazek.

Więc choć interpoluj mój świat... or something

Shader może kolorować na przeróżne sposoby, zależne od kreatywności developerów, ale zwykle zawiera on kod, który odpowiada za teksturowanie, oświetlenie, cienie itd. Co ciekawe, długość kodu shaderów wydaje się odwrotnie proporcjonalna do ilości kolorów w grach. Generic Military Shooter color palette… Ale to tak tytułem dygresji. Oczywiście nie jest tak, że vertex shader w tych rzeczach nie uczestniczy, bo często kawałek kodu jest tu kawałek tam, ale zawsze to we fragment shaderze wszystkie te wartości są łączone w całość.

Tym niemniej, zwykle dobrze jest umieścić kawałek oświetlenia, czy czegokolwiek innego, w vertex shaderze, a kawałek w pixel shaderze. Przede wszystkim dlatego, że fragment shader wykonywany jest wielokrotnie więcej razy niż vertex shader, a czasami nie jest potrzebna dokładność per-pixel. Czasem wystarczy obliczyć wartość w werteksach, a następnie pozwolić karcie graficznej ją interpolować. Dzięki temu oszczędzamy ułamki sekund na wykonywaniu dodatkowego kodu w fragmentach, ponieważ interpolacja na karcie graficznej jest kosmicznie szybka.

Tak jak w wypadku vertex shadera wartością wynikową są współrzędne dokładnie jednego werteksu w przestrzeni kamery, tak fragment shader wypluwa z siebie dokładnie jeden kolor, który może (ale nie musi) stać się barwą pixela na ekranie. Czasem mogą być dwa (z większą ilością się osobiście nie spotkałem, ale kto wie), ale ten drugi trafia na zupełnie odrębny obrazek, który może być kreatywnie wykorzystany przez programistę, ale na ekran bezpośrednio nie zostanie wstawiony.

Texture me plenty!

Mówiłem sporo o tym, że jednym z ważniejszych i najczęściej pojawiających się parametrów w werteksach są koordynaty tekstur. Czym to się je i jak owija się tekstury wokół modeli 3D? Wszystko zaczyna się od tzw. UV mappingu, czyli rozkładania mesha „na płasko”. To jest proces, który można porównać do modelarstwa kartonowego, z tym że zamiast przechodzić od płaskiego arkusza do trójwymiarowego modelu, poruszamy się w kierunku odwrotnym.

Chyba najbardziej znienawidzona część pracy grafika. Enjoy...

UV mapping często przeprowadza się ręcznie w edytorze 3D i… większość grafików serdecznie tego nienawidzi. To strasznie żmudne i frustrujące zajęcie. Powyżej macie sześcian, który pociąć i rozpłatać można z zamkniętymi oczami, ale jeśli pomyśli się, że to mógłby być np. model człowieka albo jakiegoś innego organicznego obiektu, np. smoka, to już tak prosto nie jest. Co gorsza, to nie jest origami — tutaj w ruch idą nożyczki. Miejsca, w których krawędzie (odcinki między werteksami) są przecięte i zaburzona jest ciągłość rozłożonej siatki nazywa się szwami (ang. „seam”). Mają one tą irytującą cechę, że je widać. Zapewne zauważaliście je wielokrotnie w grach. Za ich ukrycie odpowiadają w dużej mierze graficy 2D tworzący teksturę na bazie rozłożonej siatki, jednak rola właściwego UV mappingu również jest niebanalna, bo trzeba się postarać by szwy nie wypadały w najbardziej widocznych miejscach.

Na całe szczęście można to również zrobić automatycznie. Oczywiście najczęściej rezultaty są dalekie od doskonałości, ale czasem mogą stanowić dobrą bazę dla dalszej pracy. Można też, przy wykorzystaniu Waszych ulubionych przekształceń, np. wygenerować koordynaty tekstur dynamicznie, tworząc chociażby obrazek poruszający się po jednym obiekcie zgodnie z ruchem innego obiektu. A jak takie koordynaty wyglądają?

Otóż są to zwyczajne dwówymiarowe wektory. Działa to tak, że każdy werteks, poza swoimi współrzędnymi w przestrzeni 3D, ma przypisane współrzędne na dwuwymiarowej płaszczyźnie UV. W tej płaszczyźnie najważniejszy jest jej wycinek wyznaczający kwadrat o boku 1. Ten kwadrat wyznacza granice tekstury, która zostanie nałożona na obiekt. Jak zapewne się domyślacie, w tym miejscu jej rozdzielczość nie ma najmniejszego znaczenia, gdyż przekłada się ona tylko na „gęstość” pikseli, a nie na zakres współrzędnych UV — dzięki temu nie trzeba przerabiać rozkładu od nowa przy okazji zmian rozdziałki nałożonej tekstury. A co jeśli kawałek rozłożonej siatki wystaje poza obręb rzeczonego kwadratu? Wtedy możliwości jest kilka. Tekstura na krawędziach kwadratu może być odbita, powielona (kafelkowanie) lub może jej tam nie być, a jej miejsce zajmie wtedy jakiś ustalony kolor-wypełniacz.

Dobra, a Dlaczego UV? Żeby się nie myliło z XYZ, zarezerwowanymi dla ważniejszego, trójwymiarowego świata gry. Ot, wszystko.

W vertex shaderze wyznaczane są koordynaty tekstur dla werteksu — oczywiście nie są one przekształcane do żadnych przestrzeni, gdyż nie ma takiej potrzeby (tzn. są już wyznaczone w jedynie słusznej dla siebie przestrzeni), ale można je zmodyfikować wedle potrzeb (np. animując teksturę) lub wygenerować proceduralnie albo losowo. Te współrzędne są następnie interpolowane dla danego fragmentu i przekazywane do fragment shadera.

We fragment shaderze programista wywołuje funkcję, której atrybutem są współrzędne UV, a wynikiem kolor leżący na teksturze w tym konkretnym miejscu. Tutaj, jednakże, również następuje interpolacja, ponieważ tekstura może być rozciągnięta lub pomniejszona, co karta graficzna musi wziąć pod uwagę jeśli nie chcemy uzyskać Ataku Wielkich Pikseli. Oczywiście kiedy tekstura na ekranie rozciągnie się wystarczająco, to uzyskamy w zamian efekt plamy z budyniu, ale z dwojga złego…

Lewo: Brak filtra, Prawo: Interpolacja liniowa

Kiedy już mamy kolor z tekstury, możemy go pomnożyć przez lub dodać do różnych innych kolorów — np. koloru obliczonego dla oświetlenia dynamicznego, statycznego, ambient probes czy wspomnianego koloru interpolowanego z atrybutów werteksów. Możliwe jest też, że dany obiekt ma przypisanych kilka tekstur, które mogą się na siebie nakładać, często z uwzględnieniem przezroczystości. Najważniejsze oczywiście w tym wszystkim jest oświetlenie, jednak ono zasługuje na całkowicie osobny tekst w tym cyklu.

Fragmentaryczna głębia prymitywów

I tak udało nam się wyrenderować pojedynczy fragment na prymitywie wchodzącym w skład jednego modelu 3D. Nie jest to jednak koniec renderingu całej sceny, gdyż wcale nie jest powiedziane, że nasz świeży kolorek trafi rzeczywiście na ekran. Dlaczego? Ponieważ to zależy od głębi fragmentu. Nie, nie emocjonalnej, choć nigdy nie wątpiłem w niezwykłą wrażliwość pikseli. Chodzi o głębię w sensie odległości od ekranu.

Poza buforem zawierającym obraz naszej gry, istnieje również tzw. depth lub Z buffer (Z ponieważ XY to, w tym wypadku, płaszczyzna ekranu). Do bufora Z zapisuje się głębię każdego fragmentu, która jest później porównywana z głębią kolejnych. Na ekran trafiają te fragmenty, które na buforze głębi wypadają najbliżej płaszczyzny ekranu. Jak zapewne rozumiecie, założenie jest takie, żeby fragmenty (i obiekty) leżące dalej od kamery nie zasłaniały tych, leżących bliżej.

„A dlaczego miałoby być możliwe, że zasłonią?”, mógłby ktoś zapytać. Otóż jest to możliwe właśnie dlatego, że rendering oparty na rasteryzacji kompletnie olewa to gdzie względem siebie znajdują się obiekty — interesuje go tylko położenie tych obiektów względem kamery. Ponadto, obiekty nie są (zwykle) renderowane „od tyłu”, czyli od najdalszego do najbliższego. Takie rozwiązanie byłoby bardzo często nieoptymalne z punktu widzenia szybkości renderingu. Bufor głębi jest więc protezą, ale jakże konieczną.

Niestety, komputer ma ograniczoną pamięć i moc obliczeniową, a to oznacza ograniczoną dokładność. Oznaką tego jest tzw. z-fighting, czyli wyświetlanie na zmianę raz jednego, raz drugiego obiektu. Dzieje się tak wtedy, kiedy różnica między głębokością dwóch fragmentów jest mniejsza niż dokładność bufora. Aby ograniczyć ten problem, a dokładniej jego uciążliwość, bufor głębi jest nieliniowy. To znaczy, że dokładność spada wraz z odległością od kamery. To chyba zrozumiałe, że z-fighting jest mniej denerwujący kiedy zdarza się 3 kilometry od nas, niż kiedy coś nam mruga tuż przed oczami. Nie oznacza to jednak, że nieliniowy bufor rozwiązuje problem w całości — czasem, niestety, do walki musi dojść, przede wszystkim wtedy, kiedy dwa trójkąty leżą na wspólnej płaszczyźnie.

Możecie się zastanawiać po co miałyby leżeć, ale takie rzeczy się zdarzają, chociażby wtedy, kiedy na jakiejś powierzchni umieszczamy tzw. decal, czyli mówiąc obrazowo „naklejkę”. Może to być np. plakat, liście na chodniku albo plama z zaschniętej krwi. Wtedy najczęściej wykorzystuje się tzw. depth bias, czyli przypisaną na sztywno do obiektu wartość, która jest dodawana do głębi każdego wyrenderowanego fragmentu. Dzięki temu, zmniejsza się szansa na z fighting z płaszczyzną, na którą nasz decal jest przyklejony, a w zamian otrzymujemy szansę, że z dostatecznie dużej odległości naklejka będzie widoczna przez… buty stojącej na niej postaci.

Bufor głębi jest silnie związany z clipping planes w kamerach. Near plane wyznacza jego początek, zaś far skrajną końcową wartość. Z tego względu ustawienie near i far jest bardzo ważne, gdyż im szerzej są rozstawione tym mniejsza gęstość bufora głębi i mniejsza jego dokładność, a co za tym idzie większa szansa na z-fighting. Założenie jest takie, żeby ustawiać te płaszczyzny najbliżej jak się da, co jednak nie zawsze jest możliwe, zwłaszcza w grach z otwartym światem, w których często możemy popatrzeć sobie na panoramę całego miasta. Jest to najgorszy scenariusz dla bufora głębi i to właśnie z tego względu z fighting zdarza się częściej w grach pokroju GTA, a zdecydowanie rzadziej w „koryto szuterach”.

Jak działa GPU, czyli mityczny wielolufowy paintball

Na koniec jeszcze dwa słowa w materii tego, jak shadery przekładają się na działanie procesorów w karcie graficznej, czyli trochę o relacji programowania do krzemu. Jak zapewne wiecie, karta graficzna jest procesorem skrajnie wielordzeniowym — np. GeFroce GTX 680 posiada 1536 rdzeni CUDA. Oczywiście wszyscy doskonale rozumieją, że ten prosty fakt przekłada się na gigantyczną szybkość obliczeń, ponieważ procesory mogą robić wiele rzeczy na raz, ale jak to się przekłada na shadery? Zapewne zauważyliście, że dość mocno podkreślałem to, iż do vertex shadera trafia zawsze jeden werteks, zaś do fragment shadera jeden zestaw parametrów dotyczących tylko jednego konkretnego framentu. Równie ważne jest to, że z fragment shadera wychodzi zawsze dokładnie jeden kolor (ewentualnie dwa, ale ten drugi dotyczy wtedy zupełnie odrębnego obrazka, który nie trafia na ekran).

Ta „izolacja” sprawia, że nie jest możliwe zaistnienie jakiegokolwiek konfliktu między shaderami wykonywanymi równolegle na różnych rdzeniach, ponieważ w danym momencie każdy werteks czy fragment obrabiany jest wyłącznie przez jeden i tylko jeden procesor (przy pomocy odpalonego na nim kodu shadera). Gdyby tak nie było, mogłoby dojść do tzw. race conditions, czyli bardzo częstego problemu trapiącego programowanie równoległe. Dzięki wyspecjalizowaniu GPU, jasnym wytycznym względem jego programowania i kilku, metaforycznie mówiąc, zatopionych w krzemie algorytmów, możliwe jest wyświetlanie cholernie skomplikowanych scen w 0.016 sekundy, czyli z prędkością 60Hz.

A teraz zapraszam na scenę naszych przyjaciół, Adama Savege’a i Jamiego Hynemana, którzy zaprezentują działanie karty graficznej i różnicę między GPU a CPU w sobie właściwym stylu — z przytupem i wielką armatą:

Oczywiście to tworzy również pewne niedogodności dla programistów, ponieważ np. we fragment shaderze nie da się sprawdzić koloru sąsiedniego fragmentu. Nie ma po prostu takiej możliwości, gdyż spowodowałoby to naruszenie zasady izolacji obliczeń. Z tego względu, jeśli chcemy zrobić jakikolwiek efekt wymagający tego rodzaju wiedzy (np. pierwszy z brzegu bloom, gdzie kolor fragmentu może „rozlewać się” na jego otoczenie), to musimy, poniekąd, wyrenderować scenę dwukrotnie — najpierw na teksturę w rozdzielczości ekranu, która nie będzie wyświetlona (jest to tzw. off-screen rendering) i którą następnie nałożymy na płaszczyznę i dopiero są płaszczyznę wyświetlimy, obrabiając jednocześnie teksturę. Tutaj już możemy już sprawdzać sąsiednie fragmenty, gdyż są one zapisane na już istniejące teksturze nałożonej na obiekt, a nie w powstającym właśnie obrazie.

I to by było na tyle… na razie

Niniejszym obwieszczam, że temat prostego renderingu mamy załatwiony. Co zostało? Oczywiście to, co sprawia, że nowoczesne gry wyglądają tak fenomenalnie — oświetlenie, cienie i podobne efekty. Oświetlać sceny w grach można na wiele sposobów i jest to naprawdę temat rzeka. Odchodzące w niepamięć światła punktowe, piękne acz statyczne lightmapy, tysiące opóźnionych świateł, odbicia udawane przez wirtualne światła (CryEngine 3) czy wreszcie oświetlenie oparte o SVO (Unreal Engine 4). Nawiasem mówiąc, czekam na odpowiedź CryTek na ten ostatni punkt z listy. Żyjemy, jak to się mówi, w ciekawych czasach w materii oświetlenia gier. Dzięki w pełni programowalnym shaderom, rozwojowi kart graficznych i pomysłowości matematyków i informatyków tworzących nowe algorytmy, stoimy na progu prawdziwych rewolucji, które sprawią (sprawiły?), że światło w grach będzie zachowywać się dokładnie tak jak można tego oczekiwać.

Ale o tym następnym razem. Do przeczytania.