Game’s Anatomy 2: Hej, pokażesz mi swoją bazę?

Witam w części drugiej, mocno spóźnionej, naszego przewodnika po anatomii gier. Tym razem będzie trochę strasznie. Nie, poważnie, będzie matematycznie. Nie, nie, zostańcie, nie uciekajcie, nie jest tak źle… to może ja wyjaśnię po co i dlaczego.

Najpierw jednak muszę napisać, że to jest bodaj trzecia inkarnacja tego konkretnego tekstu — dwie wcześniejsze zostały anihilowane. Dlaczego? Ano, jak pewnie pamiętacie, w poprzedniej odsłonie obiecałem, że następnym razem zajmiemy się tematem oświetlenia. Kiedy jednak zacząłem o tym pisać, okazało się że zwyczajnie nie da się tego zrobić z sensem, nie opisując całego procesu pojawiania się obrazu na ekranie. Te artykuły nie mają przecież na celu wyłącznie zapchania miejsca na serwisie i poprawienia moich lichych statystyk tekstowej płodności na tle pozostałych ordynatorów – ich celem jest przede wszystkim sprawienie, byście choć trochę z tego owianego aurą tajemniczości programistyczno-matematycznego świata zrozumieli. Dlatego usunąłem kupę tekstu i postanowiłem zacząć od zera. Ponownie jednak czegoś brakowało.

Matematyka -- trochę szpetna, trochę straszna, ale w sumie piękna. I, wbrew pozorom, ma też ludzką twarz.

Grafika komputerowa to matematyka. Głównie algebra liniowa i geometria. Nie da się (a przynajmniej tak wynika z moich prób) pisać o tym jak działa grafika, nie odwołując się do przynajmniej kilku pojęć z algebry liniowej. To oczywiście nie oznacza, że potrzeba Wam wiedzieć co znaczy homomorfizm przestrzeni liniowych nad ustalonym ciałem. Absolutnie i kategorycznie nie. Ja nie mam bladego pojęcia co za czarna magia kryje się pod pojęciem homomorfizmu (choć, jak znam matematykę, jest to w gruncie rzeczy bardzo proste), ale kompletnie w niczym mi to nie przeszkadza. I poniekąd właśnie o tym nieprzeszkadzaniu jest ten cykl – ma Wam przybliżyć minimum tego, co jest konieczne, byście faktycznie rozumieli co dzieje się na ekranie i pokazać, że skomplikowanie tych wszystkich rzeczy jest w dużej mierze pozorne.

Kiedy więc zacząłem pisać o renderingu natychmiast okazało się, że jeśli powyższy cel ma mieć szansę realizacji, to bez algebry ani rusz. Dlatego właśnie ten tekst przybliży Wam kilka pojęć, którymi chcąc nie chcąc będę musiał operować w kolejnych (o ile po tym pozwolicie mi jeszcze coś napisać, haha). Obiecuję jednocześnie, że całe tłumaczenie obędzie się bez wzorów i liczenia (no, prawie). Wymagana jest tylko wyobraźnia. Najlepiej, oczywiście, przestrzenna… pun intended.

Zanim jednak przejdziemy do algebry zacznijmy od czegoś na rozgrzewkę, czyli od podstawowych części składowych świata egzystującego na karcie graficznej – wierzchołków i prymitywów.

Atomy wirtualnego świata

Wierzchołki — początek wszystkiego

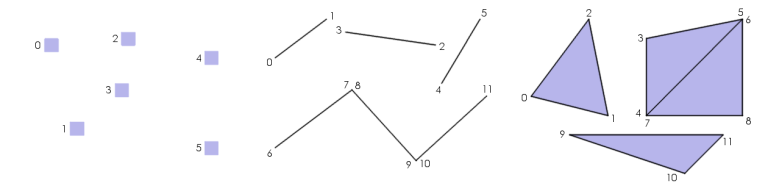
Wierzchołki inaczej zwie się z angielska werteksami. Zwykle poświęca się im mniej uwagi niż trójkątom, które z nich powstają, ale niesłusznie. Owszem, najczęściej to właśnie trójkąty (w ilościach przemysłowych) podziwiamy w grach, ale to wierzchołki są cząstkami elementarnymi wirtualnego świata na Twoim monitorze. Czym więc jest wierzchołek? Po prostu punktem w trójwymiarowej przestrzeni (liniowej), do którego można przypisać określone parametry.

Tych parametrów może być dowolna ilość, a ich wartościami są zawsze wektory (dwu-, trzy- lub czterowymiarowe) lub skalary (w razie gdyby ktoś nie pamiętał z liceum, nie chodzi o rybki akwariowe a o zwykłe liczby). Co można upchać w takich parametrach? Obowiązkowo każdy werteks musi, naturalnie, mieć parametr określający jego współrzędne X, Y i Z.

Inne powszechnie pojawiające się parametry to kolor (jako RGBA), koordynaty tekstur (tzw. texcoord) oraz trzy bardzo istotne wektory, bez których nie ma nowoczesnego oświetlania — normalna, styczna i binormalna. Szczerze mówiąc, osobiście nie wyobrażam sobie nazywania ich w ten sposób, więc przejdźmy w tej materii na jedyny słuszny język, czyli angielski – normal, tangent, binormal. Do czego służą? Otóż stanowią one (nie przestraszcie się) bazę przestrzeni tangentowej. Co to jest przestrzeń i baza przestrzeni dowiecie się za dosłownie kilka chwil. Co to jest konkretnie przestrzeń tangentowa oraz do czego i dlaczego jest potrzebna opiszę natomiast w jednym z kolejnych artykułów. Póki co powiem na jej temat tylko tyle, że jest ona podstawą normal mappingu (a więc mapowania wypukłości) i bez niej byłby on, przynajmniej w grach, całkowicie niemożliwy, co byłoby ogromną stratą — przecież to właśnie on odpowiada za dużą część detali obecnych w naszych wirtualnych światach.

Prymitywy, czyli najprostsze co da się pokazać

Kiedy już mamy grupkę zdefiniowanych werteksów wraz z całą menażerią parametrów, to możemy zacząć je konstruktywnie wykorzystywać, a więc zbudować z nich tzw. prymitywy. Są to swego rodzaju pojemniki na werteksy, które to pojemniki umożliwiają wyświetlanie wierzchołków w konkretny sposób i w konkretnych konfiguracjach.

Punkty, linie i trójkąty

Najprostsza kategoria prymitywów wyświetla pojedyncze, niepowiązane ze sobą punkty — wierzchołki „luzem”. W ten sposób wyświetlane są najczęściej werteksy w programach do edycji grafiki 3D – żeby można je było zaznaczać i nimi poruszać. Po prostu każdy wierzchołek, niezależnie od pozostałych, otrzymuje swoją graficzną reprezentację (najczęściej) w postaci kwadratu, którego rozmiar na ekranie jest niezależny od odległości kamery od tego wierzchołka (nawet jeśli używamy kamery z perspektywą).

Druga kategoria to odcinki, czyli zestawy dwóch połączonych wierzchołków. Podobnie jak w wypadku punktów, odcinki mają ustaloną grubość, która jest niezależna od perspektywy — odcinek o grubości 10 pikseli zawsze ma 10 pikseli na ekranie, niezależnie czy kamera jest od niego oddalona o 2 centymetry czy 2 kilometry — perspektywie podlega natomiast jego długość. Z tego względu zastosowania takich odcinków są raczej ograniczone, bo nie ma sensu np. budować z nich lin, co inaczej wydawałoby się logicznym zastosowaniem. Chyba, że w grze typu 2.5D.

Tutaj jedna uwaga: Jeśli dokopiecie się do jakiejś konsoli (inaczej terminala) wbudowanego w grę dla potrzeb developerów, to często znajdziecie tam możliwość włączenia tzw. widoku wireframe. Taki sam widok można włączyć w każdym edytorze 3D czy edytorze map (jak UDK czy Unity3D). Być może po przeczytaniu powyższego opisu taki widok przyszedł Wam na myśl, ale to, co wtedy widzicie to zwykle nie są odcinki takie, jak rozumie je silnik (renderer), a jedynie trójkąty z wyłączonym wypełnieniem.

Trzecia grupa to ta najbardziej powszechna, czyli trójkąty. Każdy trójkąt zbudowany jest z 3 wierzchołków (O rly?! – pomyślał Czytelnik), a przestrzeń między tymi wierzchołkami jest zwykle wypełniona wyznaczonym przez nie wycinkiem płaszczyzny. Do wyznaczenia płaszczyzny w przestrzeni 3D potrzebujemy bowiem dokładnie 3 punktów. Każdy kolejny będzie nadmiarowy i będzie wyznaczał z pozostałymi kolejne płaszczyzny, ale wcale nie musi leżeć na tej samej, co pierwsze trzy. Jeśli zaś mamy dokładnie trzy punkty, to mamy też pewność, że zawsze wyznaczą nam one wspólną dla nich wszystkich płaszczyznę — niezależnie od ich wzajemnego położenia! Jedynym wyjątkiem, naturalnie, jest sytuacja, w której wszystkie trzy leżą na tej samej prostej. To właśnie dlatego trójkątów używa się jako podstawowego budulca modeli 3D, których powierzchnie składają się wszak z wycinków płaszczyzn.

To, że obecnie korzysta się z powyższych rozwiązań nie oznacza, że są to jedyne możliwe cegiełki, z jakich można budować modele 3D. Z zupełnie innego rozwiązania korzystała, na przykład, pierwsza karta graficzna NVidii — nie będę go opisywał, bo mimo teoretycznych zalet okazało się kompletną klapą i niewielkie są szanse, by ktokolwiek do niego wrócił. Przyszłość będzie prawdopodobnie należeć do SVO, czyli sparse voxel octree, ale o tym porozmawiamy pod koniec niniejszego cyklu.

Algebra liniowa – oswajamy bestię

Algebra liniowa, przynajmniej z utylitarnego punktu widzenia, to po prostu pewne rzeczy, które da się robić w i z przestrzeniami (liniowymi, a jakże), dlatego w tym rozdziale postaram się prostym językiem opisać jak działa przestrzeń, jak się ją wyznacza i co to właściwie jest wymiar przestrzeni.

Przestrzeń i wymiar przestrzeni

Zacznijmy od tego ostatniego, bo tak wydaje się najprościej. Obrazowo, nieprecyzyjnie, błędnie i za razem całkowicie wystarczająco poprawnie (jak na nasze potrzeby) mówiąc, jest to ilość prostych jakie można poprowadzić przez jeden punkt tak, że te proste się nie pokrywają i wszystkie są do siebie wzajemnie prostopadłe. To chyba najbardziej odpowiednia „popularnonaukowa” definicja jaka przychodzi mi go głowy. Jeśli pomyśleliście o narysowanym na tablicy układzie współrzędnych, to właśnie o coś takiego chodzi. Jeżeli w przestrzeni takich prostych da się poprowadzić 2, to przestrzeń jest 2D, jeśli 3, to 3D, jeśli 1984, to jest to przestrzeń 1984-wymiarowa.

Baza przestrzeni 3D (kolory oznaczają osie: RGB = XYZ)

Teraz jak działa przestrzeń? Nieformalna definicja przestrzeni brzmi tak: Przestrzeń liniowa (inaczej wektorowa) to zbiór wektorów wraz ze zdefiniowanymi dwoma działaniami – dodawaniem i mnożeniem. Jak zapewne rozumiecie, to zwykle oznacza również obecność odejmowania i dzielenia, bo to pierwsze to po prostu dodawanie liczby ujemnej, a to drugie to mnożenie przez ułamek. Captain obvious returns. W każdym razie, wprowadziliśmy sobie wektory.

Wektory – przypomnienie lub wprowadzenie

Ze szkoły pewnie kojarzycie je jako kreski ze strzałką na końcu, które przyprawiały Was o ból głowy, i które rysowało się w określonych wzajemnych konfiguracjach. Oczywiście nikomu nie zabronię tak o nich myśleć, ale dla własnego dobra przestańcie. Wektor to po prostu zestaw liczb, z którym można robić określone rzeczy. Jakie rzeczy? Dodawać oraz mnożyć przez skalary lub przez inne wektory.

Tutaj uwaga względem nazewnictwa – mnożenie wektora przez liczbę nazywa się mnożeniem przez skalar, podczas gdy mnożenie wektora przez inny wektor nazywa się iloczynem skalarnym. Tak oto matematycy ułatwiają sobie życie i unikają nieporozumień… Z powyższego względu, polecam korzystać z angielskiej nazwy tego ostatniego: dot product. Jest ładniejsza, krótsza i mniej myląca. Tak więc mamy dodawanie wektorów, mnożenie przez skalar (liczbę) oraz dot product. Wyglądają one tak:

1. Dodawanie wektorów: (0, 1, 2) + (3, 4, 5) = (3, 5, 7)
2. Mnożenie przez skalar: (1, 2, 3) * 5 = (5, 10, 15)
3. Dot product (iloczyn skalarny): (0, 1, 2) * (3, 4, 5) = 0 * 3 + 1 * 4 + 2 * 5 = 0 + 4 + 10 = 14

Jak widzicie, produktem dodawania dwóch wektorów lub pomnożenia jednego przez liczbę są wektory, podczas gdy dot product daje nam skalar. To ważne ze względu na zastosowania tych działań, o których później. W tym tekście pojawi się tylko jedno z zastosowań pierwszych dwóch działań, podczas gdy dot product doczeka się swoich 5 minut w blasku fleszy w kolejnych artykułach.

Zasadniczo należałoby to wyjaśnić na literkach, ale niektórzy mogą mieć z tym związane złe wspomnienia, więc myślę, że taki przykład powinien być wystarczający.

Baza przestrzeni, czyli skąd wziąć wszystkie jej punkty

Anyway, wyobraźcie sobie, że na wspomnianych wcześniej prostych ustawiacie wektory jednostkowe (czyli długości jednej jednostki) – na każdej prostej po jednym, a każdy z początkiem w tym samym punkcie (jak na ilustracji powyżej). Ten punkt staje się punktem (0, 0, 0) naszej przestrzeni, czyli jej początkiem, a wektory mają współrzędne (1, 0, 0), (0, 1, 0) oraz (0, 0, 1).

Te 3 wektory nazywane są bazą przestrzeni i wyznaczają nam naszą przestrzeń liniową. To znaczy, że jeśli pomnożycie sobie te wektory przez skalary (liczby), a następnie dodacie do siebie wektory wynikłe z tego mnożenia, to możecie w ten sposób wyznaczyć (inaczej znaleźć) dowolny inny wektor (i dowolny punkt) w przestrzeni. To jest w zasadzie matematyczny odpowiednik zapisania wektora na kartce — w ten sposób algebra wypełnia sobie wektor współrzędnymi. Przykładowo, załóżmy że chcę aby moja przestrzeń odnalazła w sobie punkt (7, 10, 3). Zapisanie go to nie problem — podobnie jak jego „skonstruowanie” z wektorów bazowych. Popatrzcie (pamiętajcie o kolejności wykonywania działań — tu też obowiązuje ;) ):

(1, 0, 0) * 7 + (0, 1, 0) * 10 + (0, 0, 1) * 3 = (7, 0, 0) + (0, 10, 0) + (0, 0, 3) = (7, 10, 3)

Oczywiście możecie zapytać po co tyle zachodu, skoro współrzędne można po prostu zapisać i wsio. Jest to ważne, bo z wektorami bazowymi można robić różne ciekawe rzeczy, które powinny przekształcać (zapamiętajcie to słowo) całą przestrzeń, którą te wektory wyznaczają (względem innej przestrzeni). To znaczy, że kiedy je zmodyfikujemy, to wszystkie wierzchołki, jakie sobie w tej przestrzeni zbudowaliśmy (oraz trójkąty z nich powstałe) też muszą się zmienić. Kiedy mamy bazę i dwa proste działania, dzieje się to automatycznie — obracamy wektorami bazowymi, a wszystko inne w ich przestrzeni obraca się wokół nich.

Mógłbym tu dodać (doprecyzowując tym samym definicję), że wektory bazowe są liniowo niezależne, czyli żadnego z nich nie da się wyznaczyć za pomocą 2 pozostałych. Jasne jest, że choćby nie wiem jak mnożyć i dodawać do siebie (1, 0, 0) i (0, 1, 0), nie da się uzyskać (0, 0, 1), bo jedynka w trzeciej składowej wektora musiałaby wziąć się z powietrza (mnożenia przez zero pan nie oszukasz). Jednak już każdy inny wektor, jak pokazaliśmy powyżej, da się uzyskać z tych trzech, więc tworzyłby on zależność z pozostałymi. Na tym z grubsza polega liniowa niezależność i liniowa zależność. Dlatego też w przestrzeni 3D liniowo niezależnych wektorów będzie maksymalnie 3, zaś w przestrzeni 25D – 25.

Jeśli coś z tego zrozumieliście, to powinniście też pojąć definicję wymiaru przestrzeni bliższą definicji formalnej: Wymiar przestrzeni to maksymalna ilość wektorów liniowo niezależnych w tej przestrzeni.

Przekształcenia, czyli z przestrzeni do przestrzeni przechodzenia kurs przyspieszony

No dobra, wyznaczyliśmy sobie przestrzeń i wiemy jakie działania można wykonywać na jej składowych (wektorach). To jest pierwsza przestrzeń, jaką wyznaczamy, a więc nasza przestrzeń globalna. To jest sprawa czysto umowna – po prostu na potrzeby ograniczenia „dymienia czachy” programisty umawiamy się, że ta konkretna przestrzeń wyznacza nam nasz cały Wszechświat. Dzięki temu mamy chociaż jeden zestaw kierunków i wymiarów, który możemy uznać za absolut.

Ale to nie znaczy, że wszechświat ma monopol na przestrzenie. Swoją przestrzeń lokalną posiada każdy obiekt, a zależności między tymi przestrzeniami nazywamy przekształceniami. To one sprawiają, że obiekty w grze można ustawiać w różnych konfiguracjach, animować je, a nawet zwyczajnie wyświetlać.

Zanim przejdziemy do przekształceń, drobna uwaga (dzięki za zwrócenie na to mojej, nomen omen, uwagi, Polo_tuc!). Nie utożsamiajcie obiektu (w sensie modelu 3D) z jego przestrzenią lokalną (czy też odwrotnie). Każda przestrzeń obejmuje swoim zasięgiem cały wszechświat gry i nie kończy się na obrębie obiektu, do którego jest przypisana. Z tego względu nie można powiedzieć, że jakaś przestrzeń się kończy a inna się zaczyna — one się w sobie wzajemnie zawierają. Wszystkie zawierają też dokładnie te same punkty (w sensie, powiedzmy, fizycznym), ale te punkty są inaczej podpisane — czyli mają w każdej przestrzeni inne współrzędne. Bierze się to stąd, że wektory bazowe różnych przestrzeni są względem siebie poprzesuwane i poobracane (i często również porozciągane), co oznacza że trzeba ich różne ilości, żeby dojść od punktu (0, 0, 0) danej przestrzeni do wybranego przez nas innego punktu. Pamiętajcie, że wszystkie przestrzenie obejmują sobą wszystko, a współrzędne to nic innego jak odpowiedź na pytanie „przez jakie liczby muszę pomnożyć wektory bazowe, żeby dojść w dane miejsce?”

Przekształcenie to przede wszystkim względność. Pozwala ono na „przetłumaczenie” współrzędnych punktów i wektorów z jednej przestrzeni na współrzędne drugiej, a więc poznanie współrzędnych względem dowolnego obiektu (a dokładniej, względem bazy jego przestrzeni). To ważniejsze niż się wydaje – na tym opiera się nie tylko animacja, ale nawet samo wyświetlanie świata na ekranie. Kamera musi wiedzieć co widzi i jak to wygląda, a więc musi znać położenie punktów względem jej samej. I właśnie po to istnieją przestrzenie lokalne – żeby można było mówić o względności. Każda z nich ma swój początek oraz swoje wektory bazowe — wyznaczające kierunki i jednostki długości. Tym niemniej, bez przekształceń wszystkie przestrzenie wyglądałyby tak samo — miałyby początek w tym samym miejscu, te same kierunki i te same jednostki długości. Przekształcenia pozwalają nam zobaczyć punkty „oczami” danego obiektu.

Tak więc jeśli mamy punkt, który w jakiejś przestrzeni ma współrzędne (0, 2, 0), to w innej może mieć współrzędne (-1, 3, 1), pod warunkiem, że punkt (0, 0, 0) tej drugiej przestrzeni będzie względem tej pierwszej znajdował się w punkcie (1, -1, -1), a ich wektory bazowe nie będą względem siebie obrócone ani rozciągnięte. Jak zapewne widzicie, w takiej sytuacji przekształcenie z jednej przestrzeni do drugiej będzie bardzo proste — trudniej robi się kiedy wchodzą obroty i skale.

Niezależnie jednak co zrobimy z przestrzenią względem innej przestrzeni, ona względem samej siebie nigdy się nie zmieni. Inaczej mówiąc, przestrzeń może ulec przekształceniu tylko względem innej przestrzeni. Żeby mieć tłumaczenie, trzeba mieć co i na co tłumaczyć. To ważne, bo dzięki temu wprowadzamy sobie kolejny absolut i doprowadzamy do sytuacji, w której pudełko odwrócone do góry nogami nadal wie, gdzie znajduje się jego faktyczna górna ściana, a nie musi sobie powtarzać „góra na dole, góra na dole, góra na dole”, żeby się nie pomylić. Względem pudełka jego własna górna ściana zawsze jest na górze, tak jak moja głowa zawsze jest na górze względem mojego ciała, nawet jeśli właśnie na niej stoję.

Żeby jednak pudełko wiedziało, że jest do góry dnem, a czasem może mu się ta wiedza przydać, potrzebujemy przekształcenia. Zależność tę zapisuje się przy pomocy macierzy — w gruncie rzeczy bardzo prostego matematycznego tworu, który dźwiękiem swej nazwy wywołuje popłoch u studentów.

Skąd się ją bierze nie będę tłumaczył, ale jest to zwierz o tyle ciekawy, że jeśli nasze pudełko dostanie odpowiednią macierz i wykona na niej proste mnożenie, to będzie wiedziało nie tylko to, co już wie – czyli gdzie, względem niego samego, przyklejono na nim naklejkę this way up, ale również że jego obecne położenie względem przewożącej je ciężarówki (oraz np. asfaltu, po którym się ona porusza), przeczy napisowi na naklejce. Jeśli dostanie tych macierzy jeszcze kilka, to będzie mogło nawet obliczyć swoje położenie względem pana Mietka, co nie jest wcale takie oczywiste, bo pan Mietek jest po fajrancie i jego przestrzeń lokalna jest obrócona, względem okolicznych budynków, nie tylko w osi pionowej…

Hierarchia, czyli jak przekształceniem ułatwić sobie życie

Zostawiając jednak pudełko, ciężarówkę i pana Mietka dodam, że przestrzenie lokalne, jak zapewne już się domyślacie, umożliwiają tworzenie łańcuchów połączonych obiektów. Mogę na przykład powiedzieć silnikowi gry, że obiekt A ma znajdować się na prawo od B. I choćby nie wiem co działo się z B względem C, to A względem B zawsze będzie po jego prawicy. To tak, jak z dłonią człowieka. Niezależnie jak poruszam ramieniem w barku, albo przedramieniem w łokciu, moja dłoń nadal wie, że ma się znajdować na końcu przedramienia. Orientacja przedramienia względem ramienia, czy ramienia względem reszty ciała, kompletnie jej nie interesuje – ona wie, że ma się trzymać przedramienia i kropka. Gdyby musiała cały czas martwić się swoim położeniem względem reszty ciała, to pewnie szybko by się zmęczyła i odpadła.

W rzeczywistości takie przeliczenia wykonujemy każdego dnia, kompletnie o nich nie myśląc – jesteśmy do nich ewolucyjnie przystosowani, można by rzec. Np. kiedy mówimy, że sklep jest 20 metrów na lewo ode mnie, to operujemy swoją przestrzenią lokalną i przekształcamy (bezwiednie) kierunki świata (czy, chociażby, rozmówcy) na nasze lokalne kierunki, które zmienią się kompletnie kiedy tylko się obrócimy – wtedy sklep może być przed nami, po prawej lub z tyłu. Jednocześnie czasem z operowania różnymi przestrzeniami i przekształceniami pomiędzy nimi wynikają problemy – nie wiem jak Wy, ale ja nigdy nie mogę trafić w odpowiednie miejsce kiedy ktoś na swojej twarzy pokazuje mi, gdzie się upaćkałem. Po prostu nigdy nie wiem, czy ta osoba operuje w tej chwili swoją przestrzenią, czy moją. W tym wypadku najgorsze co może się stać w razie niewłaściwego doboru przekształcenia to wytarcie niewłaściwego policzka. W grze, gdzie na przekształceniach opiera się wyświetlenie gotowego świata, problem jest znacznie istotniejszy, bo w razie pomyłki rezultat może wyglądać znacznie bardziej dziwnie niż najbardziej pomysłowe obrazy kubistów.

Podsumujmy więc ten krótki wykład z algebry liniowej (przeprowadzony, o dziwo, przy bardzo ograniczonym udziale formalnych zapisów algebry liniowej). Przestrzeń to zbiór wektorów ze zdefiniowanym dodawaniem i mnożeniem. Wyznaczają ją wektory jednostkowe prostopadłe do siebie, zwane bazą przestrzeni. Każdy obiekt ma swoją przestrzeń lokalną, a przestrzeń wszechświata gry nazywamy przestrzenią globalną. Przestrzenie lokalne i przekształcenia są ważne, bo wprowadzają względność współrzędnych i upraszczają tworzenie oraz manipulowanie połączonymi obiektami.

Dziękuję za dzisiaj i zapraszam po więcej

Mam nadzieję, że po przeczytaniu tego wszystkiego nie boli Was jeszcze głowa. Mam też nadzieje, że ograniczenia mojej wiedzy nie spowodowały wprowadzenia Was w błąd — jeśli tak, to przepraszam i mam nadzieję, że ktoś mnie poprawi. Tak czy siak, najtrudniejszą część mamy za sobą, teraz czeka nas część bardziej praktyczna, bo zaprzęgniemy przytoczone pojęcia do zrozumienia co karta graficzna, nagięta do woli programisty (i marketingowców…), robi z tymi wszystkimi matematycznymi wynalazkami. Oczywiście zostało jeszcze kilka pojęć, ale wynikają one z powyższych w sposób tak bezpośredni, że będę je po prostu wplatał w kolejne teksty — jeśli zrozumieliście dzisiejszy wykład, to z kolejnymi też nie powinniście mieć problemu.

Czym więc zajmiemy się w dalszej kolejności? Przede wszystkim będziemy kontynuować temat trójkątów i zobaczymy jak przy pomocy atrybutów przypisanych do wierzchołków pokolorować trójkąt, nałożyć teksturę na obiekt, a także dowiemy się jak wyświetlić owe trójkąty na ekranie i, co ważniejsze, jak to zrobić żeby się nie narobić. Do zobaczenia (oby szybciej tym razem).

Czy są jakieś pytania?